The main function of the NAF database is as a record of the games people have played, but it’s also possible to use the results to make a Blood Bowl ranking. Traditionally, this has been done with an Elo style ranking, which will continue, but the NAF has also implemented a Glicko rating (which is currently being updated and thus unavailable).
As of February 2018, Sann0638 has introduced yet another way to display and analyse the world-wide NAF tournament and game data using Tableau.
Elo ranking
Each coach starts with a Coach Rating (CR) of 150 for every official Blood Bowl roster. If you attend a NAF sanctioned event using a particular race, your NAF ranking for that race is then activated. When you win a game, you gain Coach Rating. When you lose a game your Coach Rating is reduced. The neat part is that your Coach Rating is adjusted based on how tough the opponent was. For example, if you lost to a very good coach then you lose less Coach Rating than if you lost to a worse coach. If you play at NAF sanctioned tournaments, then the larger the tournament, the larger the potential change in your CR.
Coach rating is calculated by a complex formula and isn’t for the faint of heart. It’s based on the Elo ranking system. Here is the formula as it stands:
Win Probability = 1/(10^((Opponent’s Rating-Your Rating)/150) + 1)
This probability is then used to recalculate each player’s rating after the match. In the equation below, players receive 1 point if they win the match, 0 if they lose, and 0.5 for a draw. Players’ new ratings are determined as follows
Player’s New Rating = Player’s Old Rating + (K-Value * (Scoring Points – Player’s Win Probability)).
The number of NAF coaches in the tournament determines K-Value in this equation. The formula is:
K-Value = (Square Root (Min(Number of NAF coaches,MAX)) ) * 2
The MAX value is the maximum number of coaches that can contribute to the K-value. The Majors have a MAX of 60 coaches, and are treated as always having 60 coaches, even if there are fewer, while non-majors have a MAX of 32.
You can find the current rankings on the Members Area, and analysis of the games and tournament information on the Tableau page.
Glicko rating (currently offline)
Glicko is an alternative rating system to Elo, which is what the NAF has been using since Griff was in short trousers. That’s not to say it’s necessarily better, or more accurate – just different. Glicko is a more complex system than Elo, in that it has 2 numbers per rating. The first, mu, is an estimate of overall ability. The second, phi, is a measure of how confident we are about that estimate.
Coaches start with a mu of 1500, and a phi of 350. We combine the two to get our final ranking. This is done by subtracting 2.5*phi from mu. This is designed to value high ability, but also to penalise when we aren’t confident about that ability. For example, a player who has only ever attended 2 tournaments and won them both 6-0-0. Where should they be rated? This method gives them a high mu, but also a high phi – meaning they do well, but need to play more to lower their phi get to the top. The only way of reducing phi is to play lots of games!
Glicko allows us to address some of the issues in Elo rankings – the first is decay. Glicko rankings are not done per game, but on a monthly basis. If a player doesn’t play in a month their phi value is slightly increased, as we are less certain of their ability. If they don’t play for several months, their phi value inflates sufficiently to send them down the rankings. However, they retain their mu, should they wish to return at a later date.
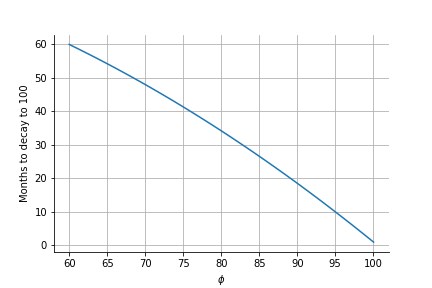
The graph below shows how phi inflates (causing rating to decay) over time (from 60 in this case).
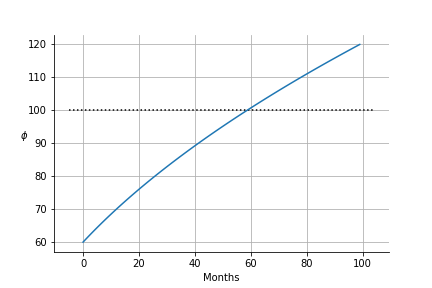
In this implementation we define coaches as inactive, if their phi exceeds 100. This means that they do not receive a rank. In real terms, it will usually take a couple of tournaments with a race before phi drops below 100, and we become confident enough of ability to provide a rank.
Decay is a fairly slow process, and playing a tournament every 18 months or so should keep you active with a particular race, so it’s not overly stringent. Inactive players/races are denoted by a “-” instead of a rank in the first column.
This graph shows how long it would take a player to decay to 100, and become inactive for different values of phi. As you can see it’s quite slow!
Another feature of Glicko is that it rewards beating coaches that have a low phi much more than coaches that are brand new and have a high value (remember phi starts at 350, and a regular tournament player may have a value around 70). This means to get to the top of the rankings, you have to beat regular players on a regular basis.
Something that does cause confusion is how many games it will take before phi decreases to below 100. The honest answer is, that it depends. If you beat a good coach with a low phi, your phi will be adjusted heavily to reflect this. Broadly your phi will decline quickly if you play low phi players, and more slowly by playing high phi players. Mubo has made a web calculator to work out your new ratings given a set of results: http://35.231.246.179/glickoweb/ (currently unavailable).
Finally, there is some cross talk between race rankings with this implementation, if a player starts a new race, they get assigned a mu depending on their existing race rankings. If a coach has a great record with other races, so we have much more confidence that he is a top Wood Elf coach too, even if this is their first tournament outing!
Global Glicko
Global glicko rankings are calculated using results pooled from all* races. The method is broadly the same, but with a small parameter tweak to make decay a little faster, as players (by definition) play at least as frequently as they do with a single race. Rankings are calculated daily, but change is expressed relative to the last full month. So, on the 30th January, change in position and rating are relative to 1st December. On the 1st Febuary, it’s relative to 1st January.
* we exclude results using the less competitive races Goblins, Halflings and Ogres.
Tableau data
All workbooks can be found on Sann0638’s Tableau page, including the NAF Report, which is also published as a PDF.
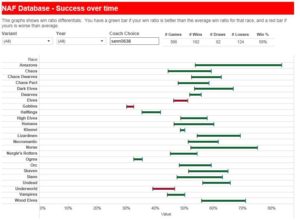
Using Tableau Public, you can view the game level data and the tournament level data. It looks a bit like this! On the games page you can find an easy-to-navigate list of all games played, which can be filtered by variant, country and year, plus a breakdown of win ratios for each race and each coach, and the grid of success for each race against each other race.
As well as that, you can now plot your (or anyone else’s) NAF rank for a given race over time, to spot the peaks and troughs of your BB career.
And if that wasn’t enough, you can enter up to 8 different coaches and see their head to head record,
There is also the differentials tab (shown in the picture above) that allows you to compare your win ratio against the average for that race, and finally a few top 10 lists of the most games played by an individual and the most games with a particular race, which can be filtered by tournaments held in a particular country. Sann0638 will be adding Nationality to these ones as well – if there are any other views you think would be good, please do comment below.
On the tournaments page you can see for the first time a collected view of the awards that have been logged on the NAF site, since the functionality to add them was added in Autumn 2017. Just the three tabs on this page, which show the records for each tournament, then the records for each coach, and then number of wins in each category starting with the most.
Additionally, just for fun, we’ve gathered together some of the most prolific coaches – those who have played at least 24 races in tournaments, and those who have played in the most countries. These can be found on the NAF Legends page!
And then, because everyone loves a map, you can see where people are playing their NAF games by going to the maps page.
And finally, with all the pages in the collection, if you want to save or share a particular view, all you have to do is scroll to the bottom and click on the share link (right). The link it produces will remember any text you have entered or filters you have applied for anyone who clicks on that particular link. You could use this to find historic pages of results for a particular tournament, or a group of club mates, or just your results with a particular race. Let us know any particularly interesting links!
The NAF hopes you enjoy these stats, which should add just a little to the BB community. Happy Blood Bowling!